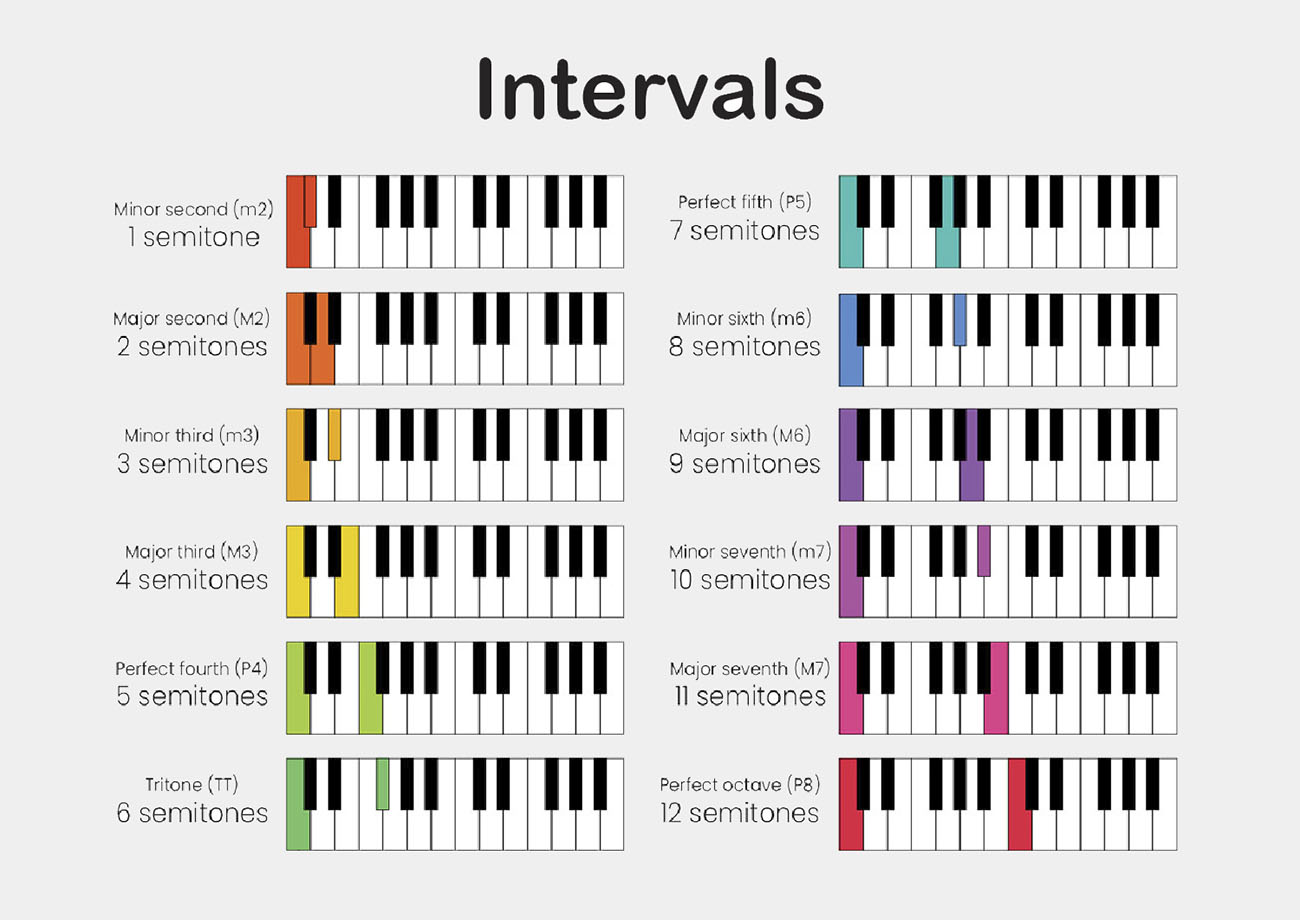
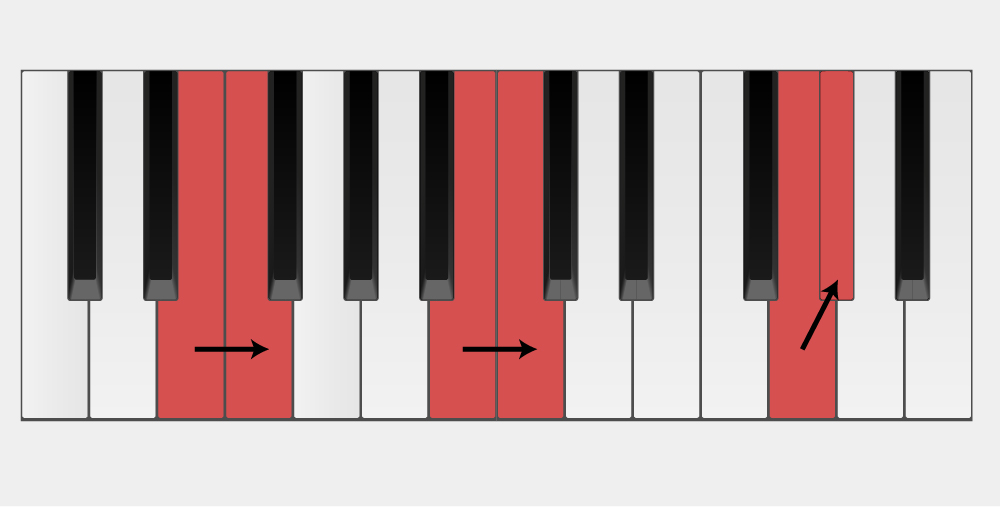
In music theory, intervals are the distances between the pitches of two notes. In Western music, there are a total of 12 different notes within an octave, so there are 12 basic types of musical intervals. Each note is the same distance from the next notes, measured in semitones or cents.
A semitone is exactly 100 cents - on the piano, a semitone step is the distance between a white key and the black key next to it, or the distance between B and C or E and F. On the guitar, each fret corresponds to a semitone step.
Why are musical intervals so important?
Each interval has its own sound and effect. Melodies are ultimately made up of intervals, so the choice of intervals has a great impact on the final result.
If I compose melodies using only perfect fifths and thirds, the melody will be beautiful, romantic or nostalgic. But if I use tritone intervals, my melody suddenly sounds creepy and scary.
Depending on which intervals I choose for my melody and how I combine them, it will have a completely different mood and effect.
But not only melodies are made of intervals, chords are too! The only difference is that in melodies the musical intervals are played one after the other (melodic intervals), while in chords they are played simultaneously (harmonic intervals).

Again, the chord has a very different effect depending on which interval combination you choose. A major chord, one of the happiest chords, consists of a major third and a major fifth, both very bright and happy intervals. A diminished chord, on the other hand, is made up of a minor third and a diminished fifth, both of which are sad and very tense intervals - accordingly, diminished chords sound very tense and sinister.
Interval names
Interval names consist of two important properties: The number and the "quality".
Interval number
Intervals in Western music are based on heptatonic scales (scales with seven steps per octave, of which 5 are whole tone steps and 2 are half tone steps. The names are derived from the Latin ordinal numbers of these steps (prima = "the first", secunda= "the second", tertia = "the third", etc.).
| Step of the scale | Designation |
|---|---|
| 1 | Prime |
| 2 | Second |
| 3 | Third |
| 4 | Fourth |
| 5 | Fifth |
| 6 | Sixth |
| 7 | Seventh |
| 8 | Octave |
| 9 | Ninth |
| 10 | Tenth |
| 11 | Undecime |
| 12 | Duodecime |
| 13 | Tredecime |
| 14 | Quartdecime |
| 15 | Fifth decimal or double octave |
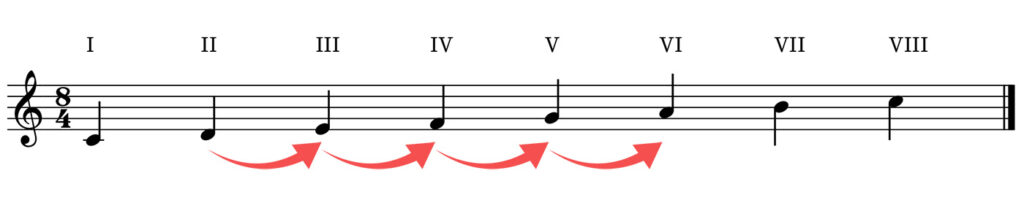
For example, "a fourth up" means the transition from one note to the note three positions higher on the scale, always using the current scale as the reference system.
For example: We are in the key of C major, and I want to go up a fifth from D. To do this, I simply have to go up 4 steps on the scale from D and end up at A.
Interval quality
Depending on how many semitones there are in the difference between our two steps of the scale, the interval is given a different name. The quality of an interval can be perfect, major, minor, augmented, or diminished.
Perfect intervals
These intervals are called like this because they are generally perceived as perfectly harmonic, although the fourth is not necessarily so. In contrast, minor, major, augmented and diminished intervals sound less harmonious.

There are 4 intervals called pure: the unison, the perfect fourth, the perfect fifth, and the octave. The unison and the octave are always perfect, as are most fourths and fifths. Perfect fourths have 5 semitones and perfect fifths have 7 semitones.
Major and minor intervals
A major interval is the larger of two possible intervals in a given key. Major intervals are the major second, major third, major sixth, and major seventh.

A minor interval is the smaller of two possible intervals in a given key. Minor intervals are the minor second, minor third, minor sixth, and minor seventh.

A second, third, sixth, or seventh is major if the higher note is in the major scale of the lower note. For example, the third between G and B is major because B is in the G major scale.
When we reduce a major interval by a semitone, the interval becomes minor. That is why the third between G and B♭ is small.
Augmented and diminished intervals
Augmented and diminished intervals occur in diatonic scales when a pure interval is diminished or augmented by a semitone. But they can also occur when small or large intervals are diminished or augmented by a semitone - but such intervals do not occur naturally in the scale.


Example: A diminished fifth (6 semitones) is created by lowering a perfect fifth (7 semitones) by one semitone. An augmented fifth (8 semitones) is created by raising the perfect fifth by one semitone.
Frequency ratios
Another important property of intervals is frequency ratio. This describes the ratio of the actual frequencies of the two tones to each other, and is calculated by dividing the higher frequency by the lower frequency.
Example: the musical note A4 has a frequency of 440 Hz, the note D5 has a frequency of 587.33. The interval between the two notes is a perfect fourth (5 semitones) and has a frequency ratio of 587.33 Hz/440 Hz = 4/3.
Here you can find the exact frequencies of all music notes.
Table of all interval names
The number and quality then give the full names of all musical intervals:
| Interval name | Halftone spacing | Frequency ratio |
|---|---|---|
| Prime/Unisono | 0 | 1/1 |
| Minor second | 1 | 16/15 |
| Major second | 2 | 9/8 |
| Minor third | 3 | 6/5 |
| Major third | 4 | 5/4 |
| Perfect fourth | 5 | 4/3 |
| Diminished fifth/Tritonus | 6 | 45/32 |
| Perfect fifth | 7 | 3/2 |
| Minor sixth/Augmented fifth | 8 | 8/5 |
| Major sixth | 9 | 5/3 |
| Minor seventh | 10 | 9/5 |
| Major seventh | 11 | 15/8 |
| Octave | 12 | 2/1 |
Of course, there are musical intervals beyond the octave, but these can be constructed by adding these 12 intervals. The semitones and cents are added, but the frequency ratios are multiplied - so they behave exponentially.
| Interval | Frequency ratio |
|---|---|
| 1 octave | 2/1 |
| 2 octaves | 4/1 |
| 3 octaves | 8/1 |
Audio examples
Here is an audio example for each interval: one as a melodic interval (two notes one after the other) and one as a harmonic interval (two notes at the same time).
| Audio example for melodic interval | Audio example for harmonic interval | |
|---|---|---|
| Minor second | ||
| Major second | ||
| Minor third | ||
| Major third | ||
| Perfect fourth | ||
| Diminished Fifth/Tritone | ||
| Perfect fifth | ||
| Minor sixth/Augmented fifth | ||
| Major sixth | ||
| Minor seventh | ||
| Major seventh | ||
| Octave |
How do I determine an interval?
Almost all intervals have a unique name, but some have several (8 semitones can be a minor sixth or an augmented fifth) - how do I find out which name is correct?
First you need to find out what key you are in. Once you know that, count from the first of the two notes (the first note is 1, the second is 2, etc.) and move up or down the scale until you reach the second note.
For example, let's take the key of D major and the notes D and A sharp. To get from D to A#, I have to go up 5 steps on the scale. But even then I don't end up at A sharp, I end up at A. So I still have to go up a semitone - so we have an augmented fifth (because fifth + semitone).
If the note were B♭ instead of A# (in practice it is the same note), because we are in E flat major, for example, we would speak of a minor sixth.
So in practice, a minor sixth and an augmented fifth are the same thing, but harmonically there is a difference. You always have to know the key to determine the unique name.
What effect do the different intervals have?
Musical intervals have different emotional effects because they each have their own unique sound.
- Unison: This interval conveys a feeling of unity and purity, as both tones have the same pitch.
- Minor second: This interval is often perceived as dissonant and tense.
- Major second: A stable but moving interval often used in melodies.
- Minor third: This interval is a fundamental component of the minor chord and is often associated with sadness or melancholy.
- Major third: An essential component of the major chord, often associated with cheerfulness or brightness.
- Perfect fourth: A stable interval that is often used in harmonies.
- Tritone: Also known as the "devil's interval", it is often perceived as dissonant and restless.
- Perfect fifth: A very stable and pleasant interval that is often used in harmonies.
- Minor sixth: A soft and rather sweet interval often used in romantic music.
- Major sixth: Similar to the minor sixth, but has a somewhat brighter, more optimistic sound.
- Minor seventh: Often perceived as somewhat restless and dissonant, it is an important component of dominant seventh chords.
- Major seventh: Can seem dissonant, but is an important component of major seventh chords and jazz harmonies.
- Octave: Like the unison, the octave conveys a sense of unity and purity because both notes have the same pitch but are in different octaves.
To illustrate the effect, let's consider two intervals that have exactly the opposite effect: the tritone (dissonant and tense) and the perfect fifth (harmonious and relaxed).
The song Black Sabbath by the metal band Black Sabbath uses the tritone interval in the guitar riff, which creates a very tense and frightening atmosphere - just perfect for dark heavy metal music.

By loading the video, you accept YouTube's privacy policy.
Learn more
In Twinkle Twinkle Little Star, on the other hand, we find a perfect fifth as the interval between the first and second "twinkle" - as you can see, this interval seems much more cheerful and relaxed. Just right for a children's song!

By loading the video, you accept YouTube's privacy policy.
Learn more
So composers choose the intervals of their melodies according to the mood or effect they want to create in the listener. If I want to create a somber, dark mood, minor seconds or tritones are appropriate intervals; but if I want to compose a happy, motivating song, intervals such as the major third or perfect fifth are best.