Circle of Fifths: Explanation, Application and Mnemonics

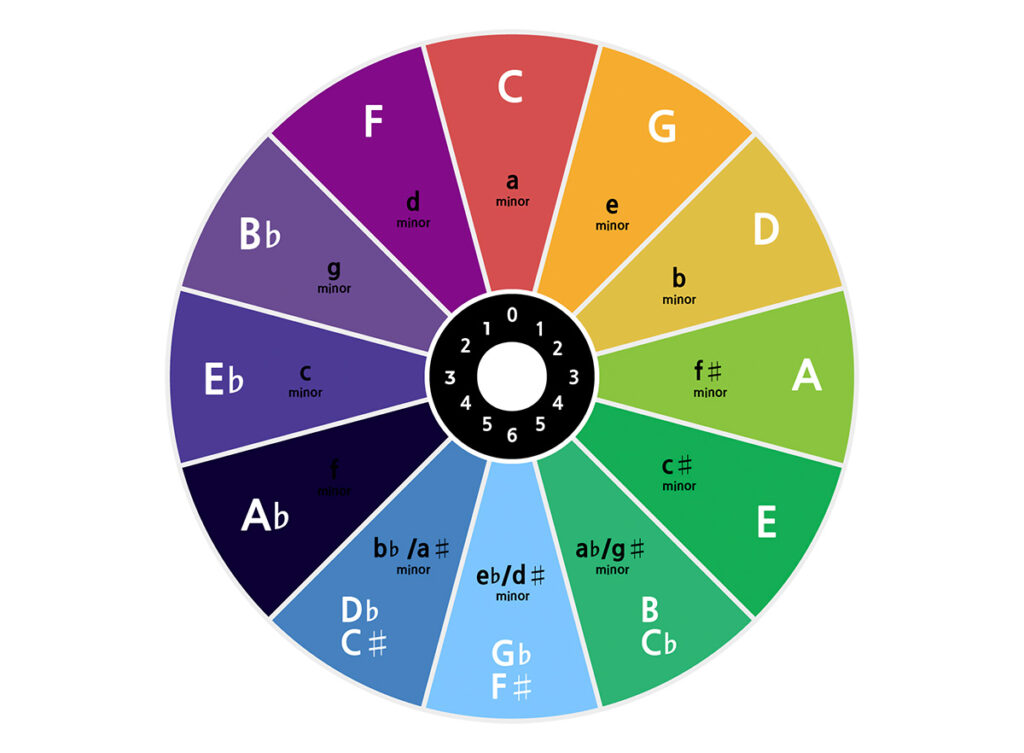
What is the circle of fifths?

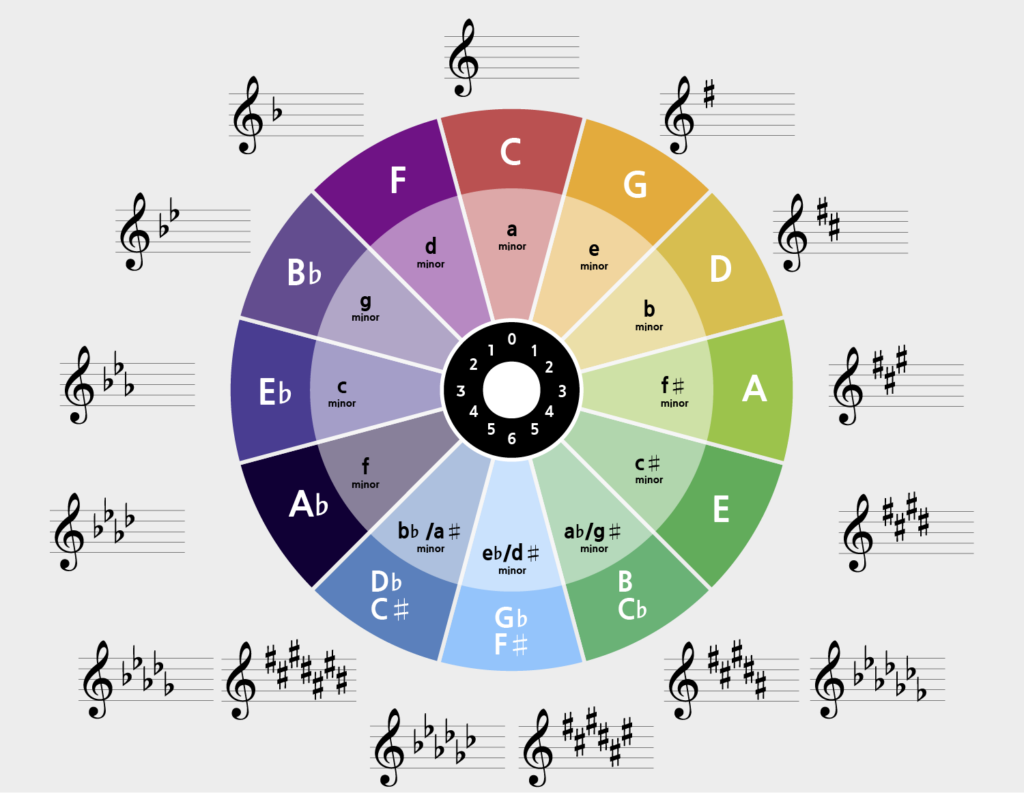
The circle of fifths (also called circle of fourths) is a graphical representation of the 12 major and minor keys in intervals of fifths, which provides a lot of information. The circle of fifths helps us to quickly identify the signatures of a key. But it also helps us build chords, find the pentatonic scale or harmonize in different keys.

You can quickly learn the circle of fifths and write it down when you need it, because each key is always one fifth away from the next - so you only have to go up one fifth (7 semitones) to get to the next key.

You always start at the top in the middle at C major and move in a circle in clockwise fifth steps. Each clockwise step means one more cross. But if you go counterclockwise in the circle of fifths, you move in intervals of fourths and with each step you add a ♭ sign.

The outer circle shows the major keys and the inner circle shows the parallel minor keys, which are always 3 semitones below the major key. This way you can quickly find the parallel keys without having to calculate.

Using the circle of fifths

Determining major keys with cross accidentals

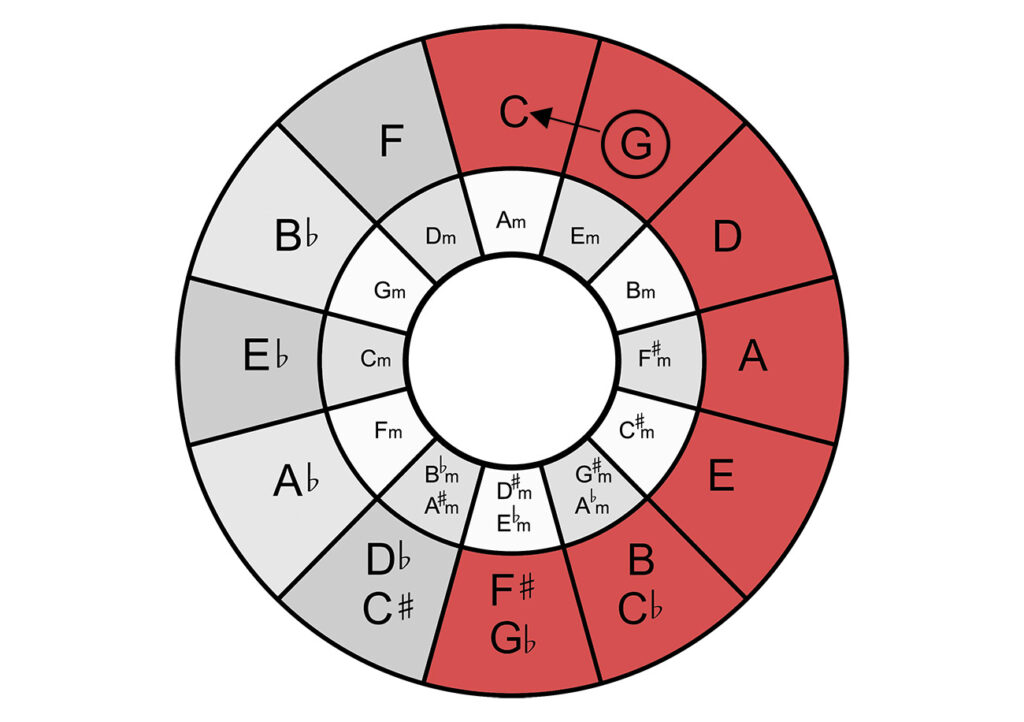
We start at the top of the circle of fifths in the middle with C major, since this key has no accidentals. From here you move clockwise to find the keys with accidentals. Each time you go one step further, you add an accidental.

key	Number of crosses	Which crosses?
C major	0	None
G major	1	F#
D major	2	F#, C#
A major	3	F#, C#, G#
E major	4	F#, C#, G#, D#
B major	5	F#, C#, G#, D#, A#
F sharp major	6	F#, C#, G#, D#, A#, E#

As you can see, the key signature is always one semitone above the last accidental - you can also work the other way around: If you only have the accidentals, but don't know the key, this is a good way to find it.

As an example: If you have 3 accidentals (F#, C#, G#), then you know the key is A major (because we move up a semitone from G# to A).

Determining major keys with ♭ accidentals

To find the keys with the sign ♭ in the circle of fifths, we start again at 12 o'clock in C major. But now we go counterclockwise (in fourths), adding another ♭ at each step.

key	Number of b's	Which ♭'s?
C major	0	None
F major	1	B♭
B flat major	2	B♭, E♭
E flat major	3	B♭, E♭, A♭
A flat major	4	B♭, E♭, A♭, D♭
D flat major	5	B♭, E♭, A♭, D♭, G♭
G flat major	6	B♭, E♭, A♭, D♭, G♭, C♭

Again, there is a trick to determining the correct key from the accidentals: The root of the key is the penultimate ♭-sign. If there is only 1 ♭-sign, it is always F major.

As an example: If there are 4 ♭-signs in our music notes (B♭, E♭, A♭, D♭), then the key is A-flat major because A-flat is our penultimate accidental.

More than 5 accidentals: Enharmonic keys

Theoretically, some keys are missing in the circle of fifths. For example, where is G sharp major or C sharp major?

These keys are represented by the corresponding enharmonic keys, which in practice contain the same notes but are named differently. For example, C sharp major would theoretically have 7 # accidentals and would be very complicated to read. The enharmonic key of D flat major, on the other hand, has only 5 B flat accidentals and is therefore easier to play, so the key with the fewest accidentals is usually chosen.

Mnemonics for the circle of fifths

With the help of mnemonics, you can quickly learn the circle of fifths. For the keys with the accidental #, remember the following sentence:

Good Dogs Always Eat Before Furry Cats

The first word starts with G, so G is first and therefore has only one cross; the second word starts with D, so D is second and therefore has two crosses; A is third and therefore has three crosses, and so on.

The following mnemonic is used for keys with a b-sign:

Five Big Elephants Are Dragging Garbage Cans

Again, the first word begins with F and is in first place, so F has only one ♭; the second word begins with B and is in second place, so B♭ major has two ♭; E is in third place, so the key has three ♭, and so on.

Determining minor keys

Minor keys lie on the inside of the circle of fifths and are always directly adjacent to the parallel major key. The minor key is always 3 semitones (a minor third) below the major key.

Minor keys have the same number of accidentals as their parallel major keys, so how can you tell which key it is by looking at the accidentals?

It is usually enough to look at the last bar of the song to see what the last note is, since this is usually the root note of the song. Songs usually end on the root note to give a sense of resolution (for more on this, see my article on musical cadences).

So if I have a piece with two crosses, I know that the key is either D major or B minor. Then I look at the last note - if it's a D, we're in D major, and if it's a B, we're in B minor.

Scale construction with the circle of fifths

➔ Click here to read the full article about musical scales

We can also use the circle of fifths to find the notes of minor or major scales.

Finding the major scale with the circle of fifths

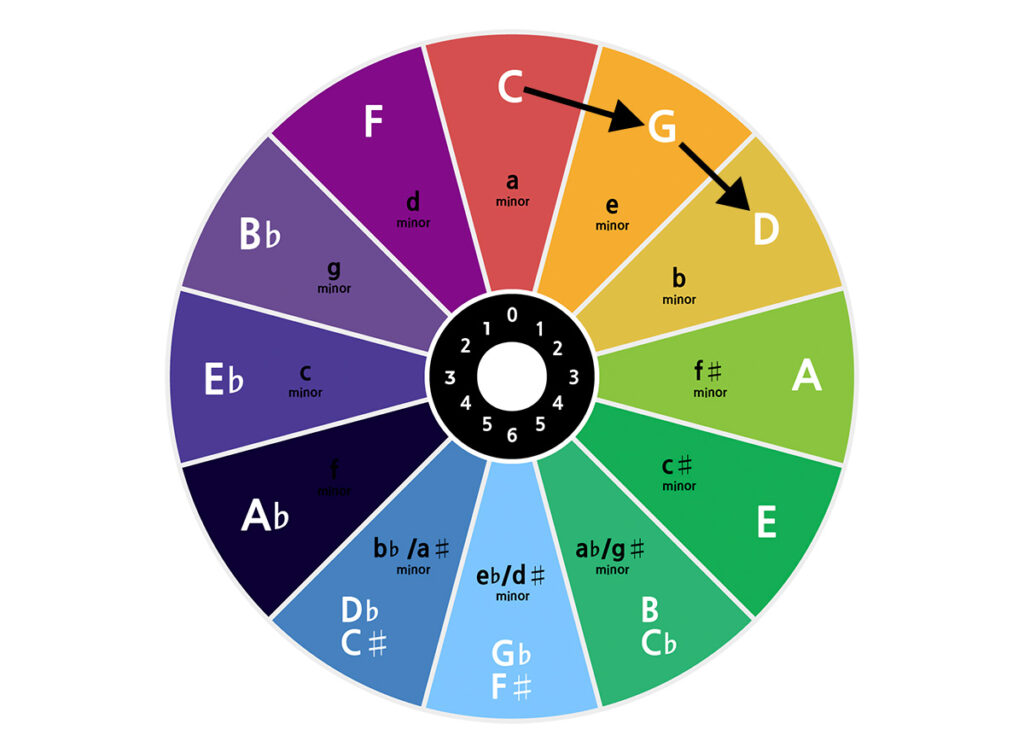
Using the circle of fifths, it is very easy to find out which notes make up the major scale. For the key of G major, for example, all you have to do is follow the steps below:

1. We are looking for the starting note, in this case G.
2. Take one step to the left (counterclockwise). In this case, you end up at C.
3. The 7 notes from C clockwise form the major scale of G.

Finding the minor scale with the circle of fifths

To get the natural minor scale, we have to work with the parallel keys again. The minor scale has the same notes as the parallel major scale, but starts on the sixth degree.

Let's take D minor as an example. To get the minor scale, do the following

1. First we look for our root on the inner circle, in this case D.
2. Then we look for the major parallel that is right next to it on the outer circle. In this case, it would be F.
3. We take one step to the left (counterclockwise), for F this would be B♭.
4. The 7 notes from B♭ clockwise are the F major scale and therefore also the D minor scale.

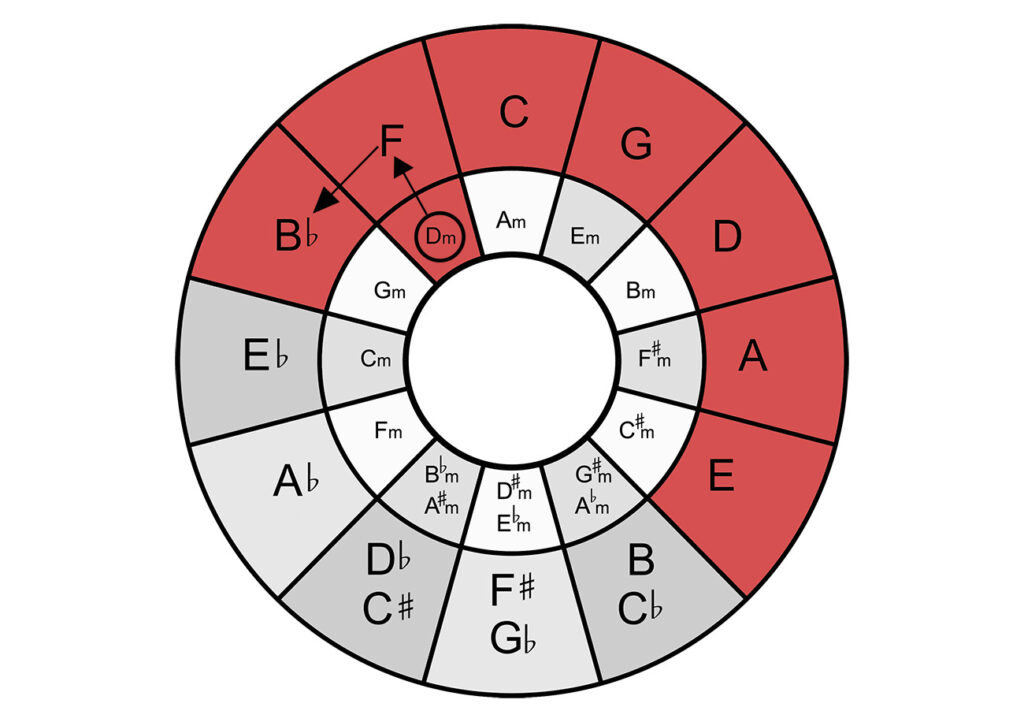
Chord construction using the circle of fifths

Before you start building chords, understand two concepts:

• A major chord consists of the root, the major third and the fifth.
• A minor chord consists of the root, the minor third and the fifth.

Building a major chord using the circle of fifths

Building a major chord is very simple, because the root and its fifth are neighbors. So you go from the root one step clockwise, and you have the fifth of the chord. To find the missing note, the third, you simply look which note is below this fifth in the inner circle (i.e. the minor parallel note).

For example, the construction of the D major chord:

1. First we look for D in the outer circle, which is our root note.
2. Its fifthis the next note when you go clockwise one step, in this case an A.
3. Its major third is right next to it in the inner circle (minor parallel tone).

So our major chord consists of D - F# - A.

Building a minor chord with the circle of fifths

Building a minor chord is also very simple if you take a closer look at the circle of fifths. The minor third is the parallel tone to the major, and the fifth is one step clockwise from the root.

As an example, let's consider the G minor chord.

1. First we look for G on the inner circle, which is our root note.
2. The fifth is found by taking one step clockwise from the root, in which case you arrive at D.
3. The minor third is the major parallel tone of the root, so we simply go outward from the root and end up with B♭ in this case.

So our minor chord consists of G - B♭ - D.

Using the Circle of Fifths to build a pentatonic scale

The circle of fifths makes it easy to find the pentatonic scales. Lets start with the major pentatonic scale.

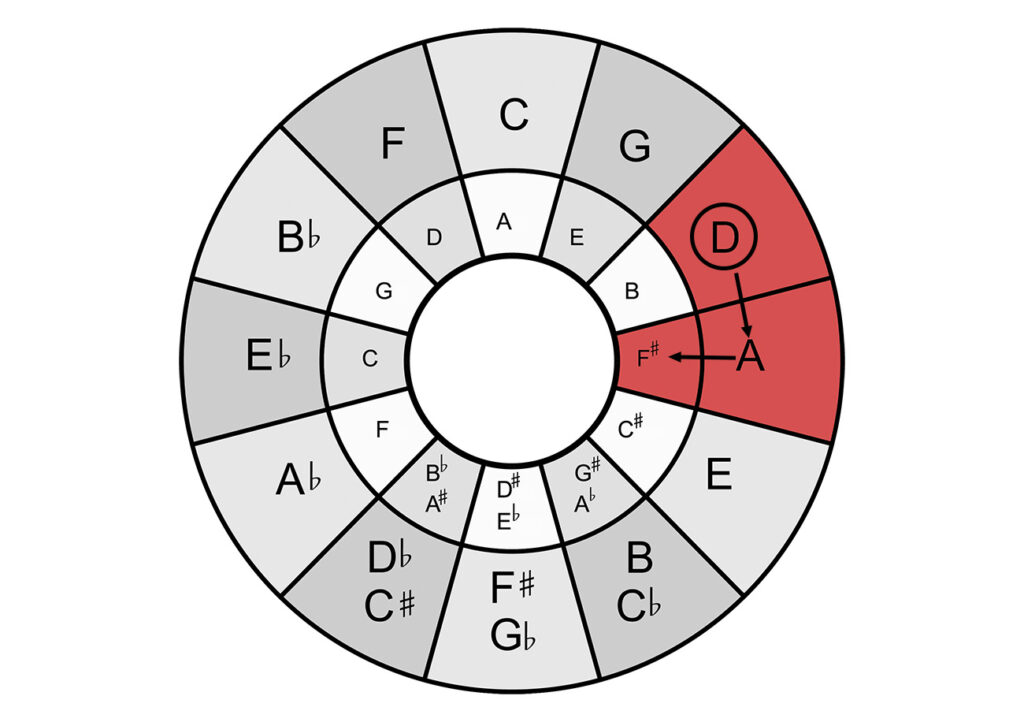
Finding the major pentatonic from the circle of fifths

To determine the major pentatonic, you need only find the fundamental in the outer circle of the circle of fifths. This and the next four notes clockwise form the major pentatonic.

For example, if we want to get the pentatonic scale of A, we look for this note in the outer circle and the following 4 form their pentatonic scale with A: A, E, B, F# and C#.

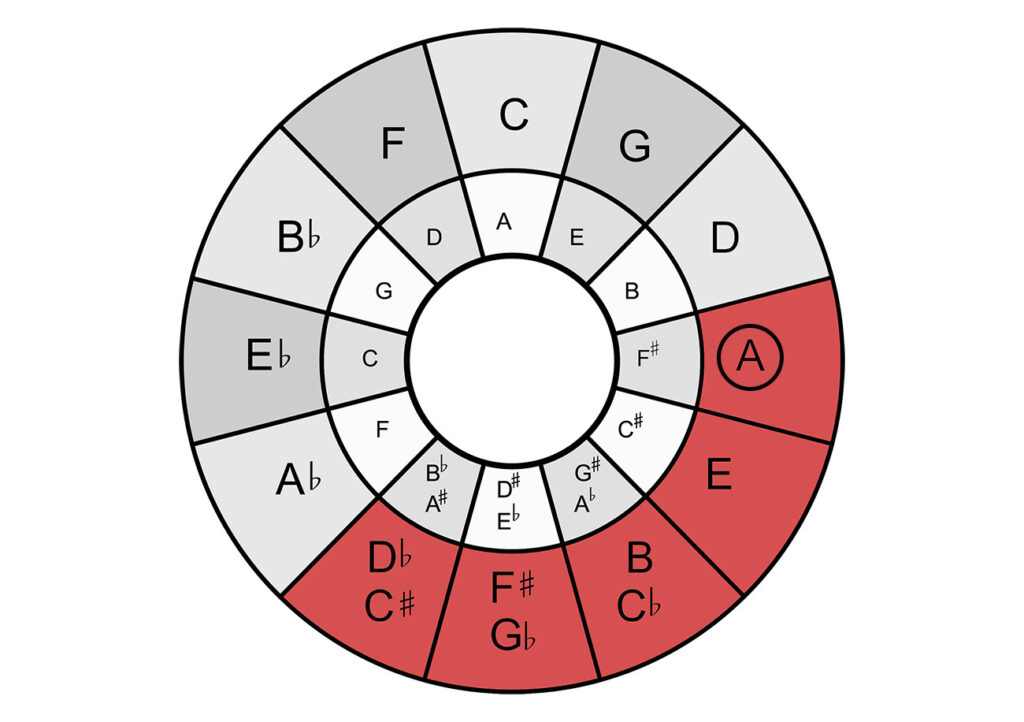
Finding the minor pentatonic scale from the circle of fifths

The process is very similar for the minor pentatonic. Since the minor pentatonic contains the same notes as the corresponding major pentatonic, you only need to perform the following steps:

1. We search for the root of the minor pentatonic we are looking for in the inner circle.
2. We take a step outward in the circle of fifths, to the parallel major.
3. Starting from the major parallel key, we count another 4 steps to the right. These 5 notes form the minor pentatonic of our starting note.

As an example, here is the identification of the pentatonic in E minor:

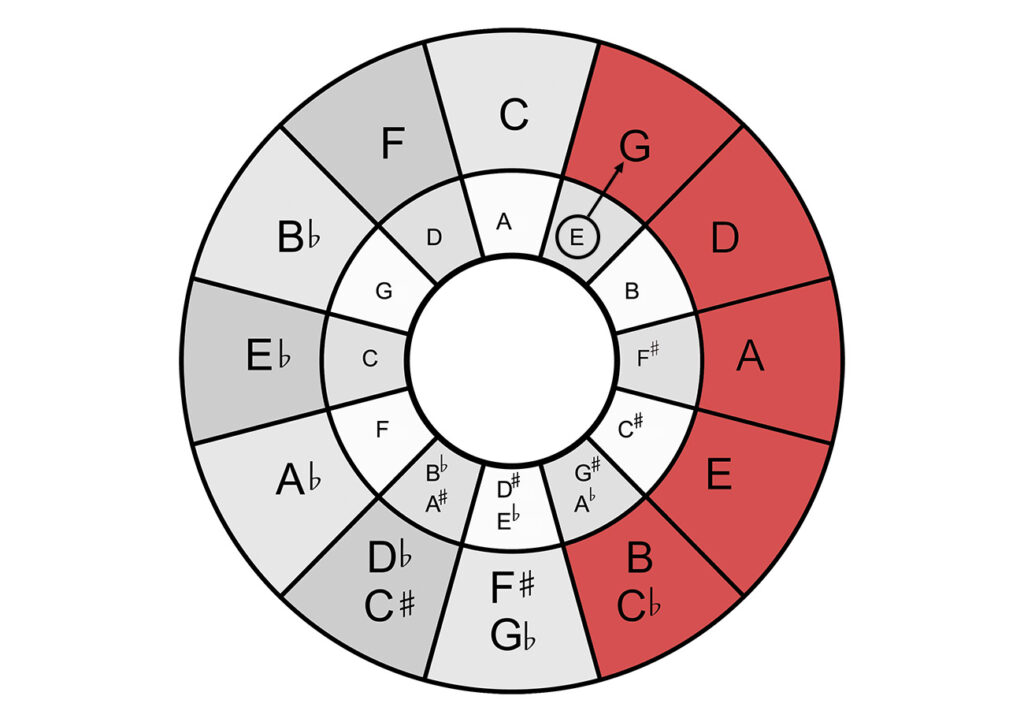
Harmonization of the major scale

The circle of fifths can do much more - it can help us find the right chords for any key, and with one simple rule you can find major, minor and even diminished chords. Since the major scale has 7 chords, you need to take 7 steps to find all the chords.

We will take the key of D major as an example:

1. First we look for the D major in the outer circle, which is our tonic.
2. The fifth degree, the dominant, is one step further clockwise, in this case A major.
3. The fourth degree, the subdominant, is one step further counterclockwise, in this case G major.
4. The second degree is the subdominant parallel, that is, the minor parallel tone of the fourth degree, in this case e minor.
5. The third degree is the dominant parallel, i.e. the minor parallel tone of the fifth degree, in our case F sharp minor.
6. The sixth degree is the parallel to the tonic, so it is on the inner circle next to the tonic. In our case, it is B minor.
7. The seventh degree is the leading tone and is to the right of the third degree, that is, to the right of our 6 minor and major chords. The seventh degree, c#, is diminished.

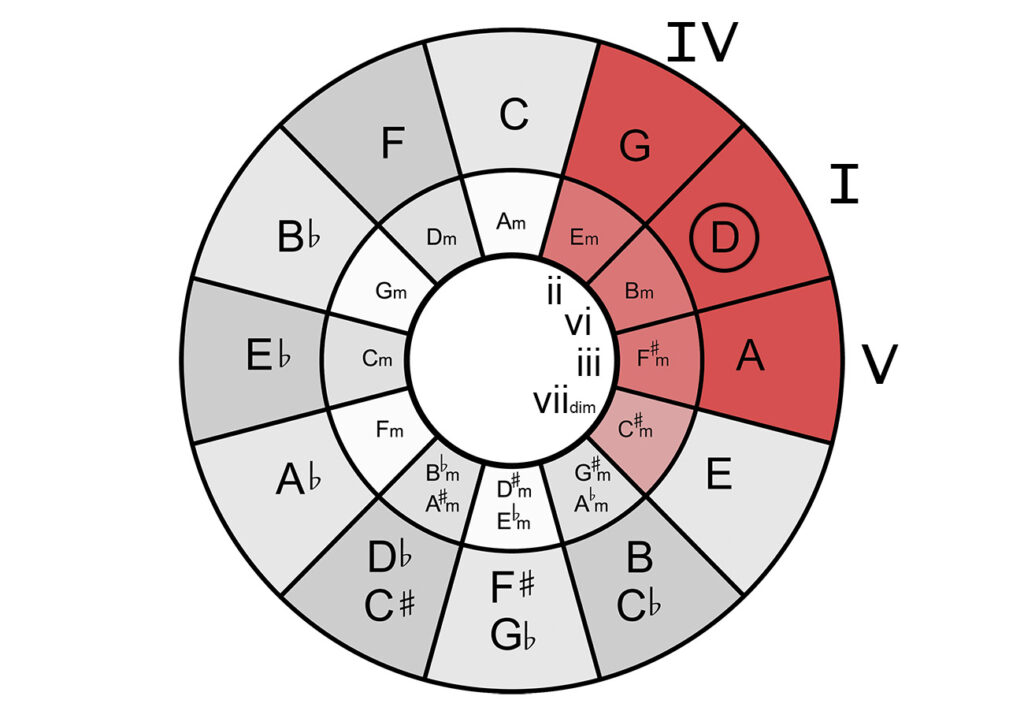
And if you look closely, it all makes sense:

• The first, fourth, and fifth degrees are major chords, so they are in the outer circle. The fourth and fifth degrees are a fifth and a fourth from the root, respectively, so they are right next to the root note.
• The second, third and sixth chords are minor chords and are located in the inner circle. They are the minor parallel chords of the first, fourth, and fifth degrees, so they are right next to them in the inner circle.
• The seventh is diminished and is in the inner circle.

By the way, the opposite notes in the circle of fifths form a tritone, the so-called devil's interval, which exactly halves the octave.

Harmonization of the natural minor scale

Harmonizing the minor scale using the circle of fifths is also child's play, and the method is very similar, if not the same, as that of major chords.

As an example, consider the harmonization of the key of E minor:

1. First we find E minor in the inner circle, which is our tonic.
2. The fifth degree (dominant), B minor, is one step clockwise away.
3. The fourth degree (subdominant), A minor, is one step counterclockwise away.
4. The sixth degree is C major, the major parallel of the fourth degree, so outside A.
5. The third degree is G major, the major parallel of the tonic, i.e. outside e.
6. The seventh degree is above the fifth degree, D major, because it is the major parallel of the fifth degree.
7. The second step, the diminished step, is the one adjacent to the fifth step: f#.

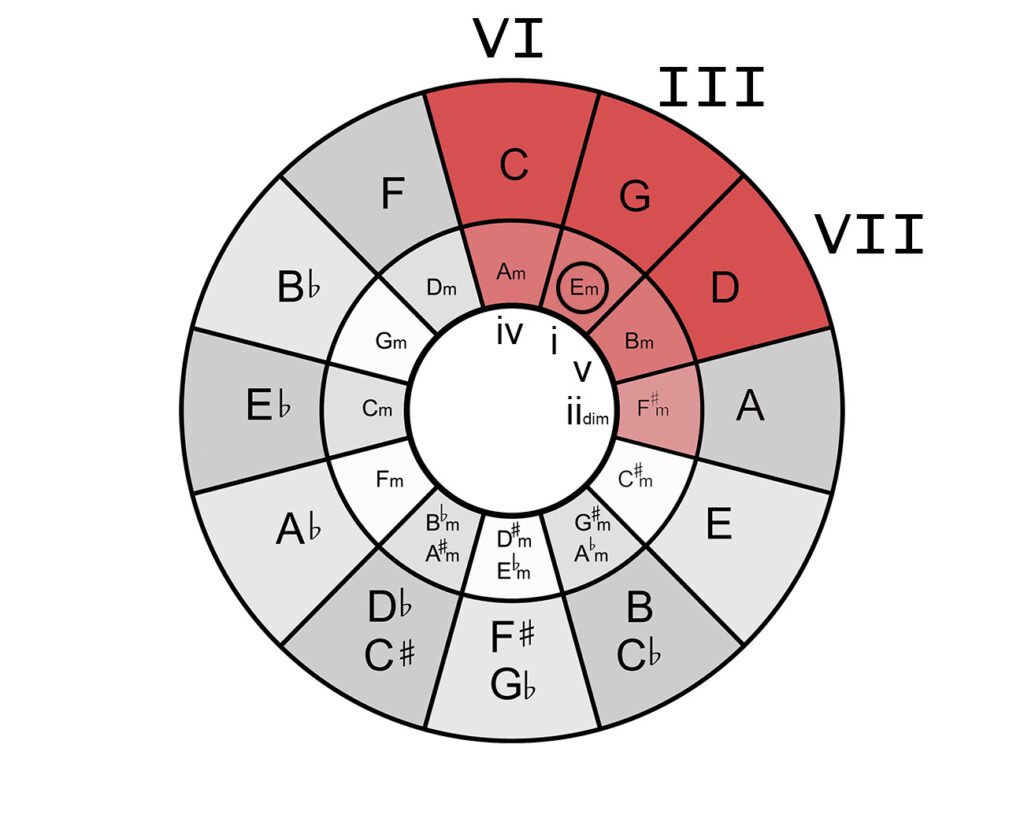
And again, it all makes sense:

• The first, fourth, and fifth degrees are minor chords, so they are in the inner circle. The fourth and fifth chords are a fifth and a fourth away from the root, respectively, so they are on either side of the root.
• The third, sixth, and seventh are major chords and are in the outer circle, directly above the first, fourth, and fifth, because these are the major parallel keys.
• The second step is diminished and is on the inner circle.

In Conclusion

The circle of fifths shows us that music and mathematics are not separate in their essence, but are expressions of the same universal principle - the search for harmony, order and beauty in the world around us. The circle of fifths is therefore more than just a tool for musicians and composers. It is a symbol of the inextricable link between art and science, emotion and logic, creativity and structure.

More articles:

• Musical syncopation easily explained
• 60 musical symbols and signs that everyone should know